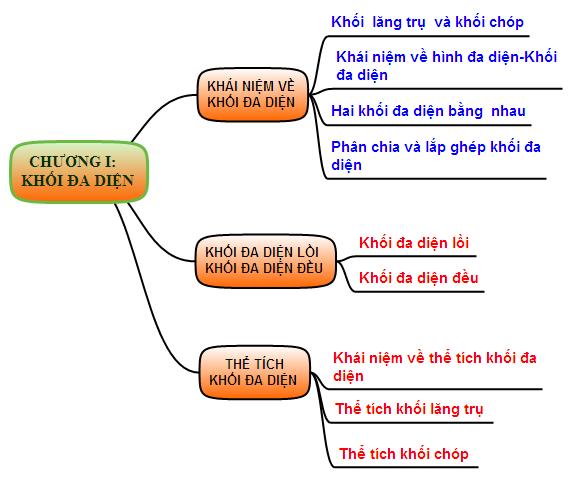
Ôn tập Hình học 12 Chương 1 Khối Đa Diện
Đề cương Ôn tập Hình học 12 Chương 1
A. Tóm tắt lý thuyết
1. Sơ đồ các công thức tính thể tích khối đa diện
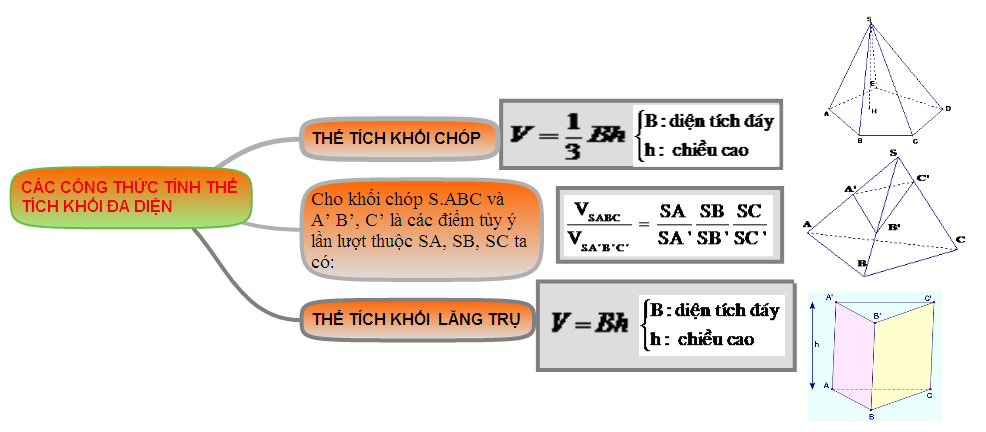
2. Hệ thống hóa kiến thức hình học không gian lớp 11
a) Quan hệ song song
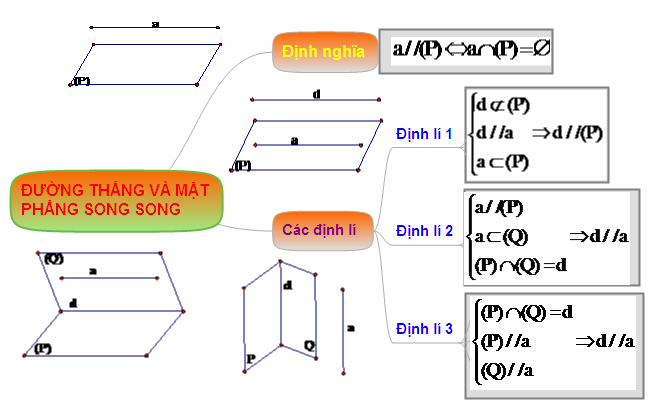
Hệ thống hóa kiến thức “Đường thẳng và mặt phẳng song song”
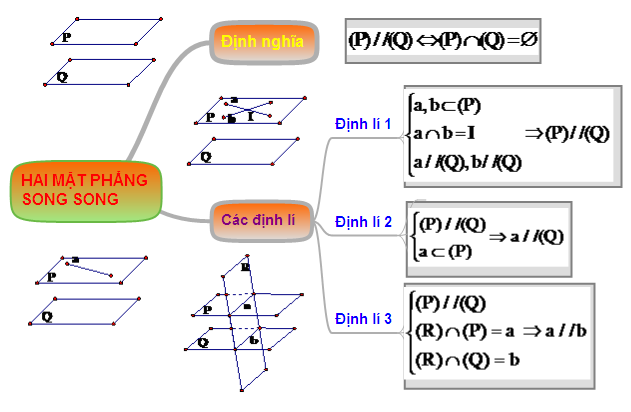
Hệ thống hóa kiến thức "Hai mặt phẳng song song"
b) Quan hệ vuông góc
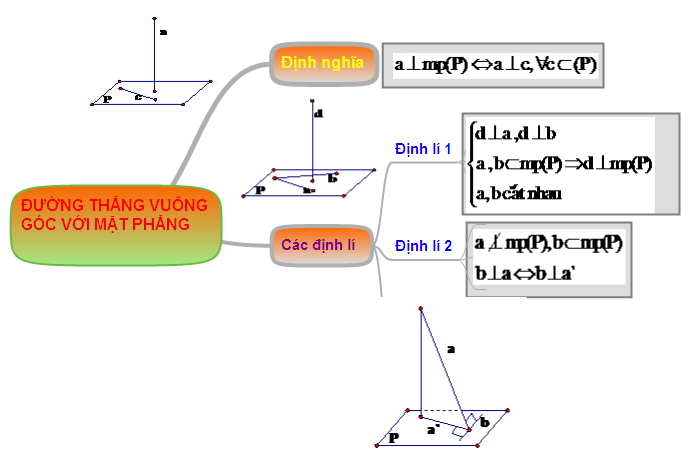
Hệ thống hóa kiến thức "Đường thẳng vuông góc với mặt phẳng"
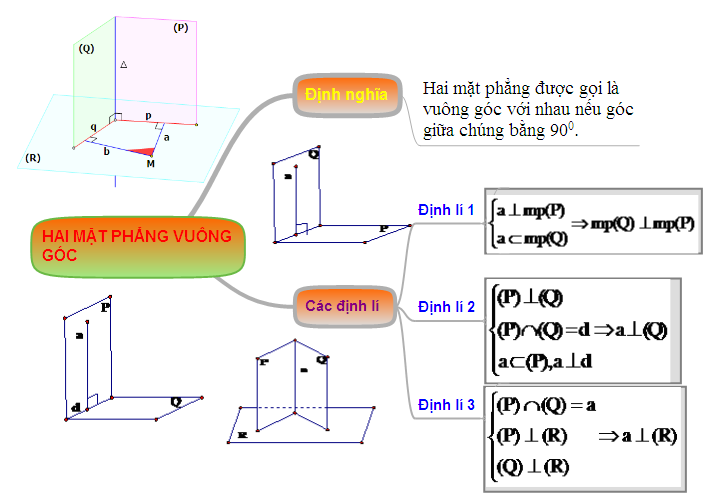
Hệ thống hóa kiến thức "Hai mặt phẳng vuông góc"
c) Khoảng cách và góc
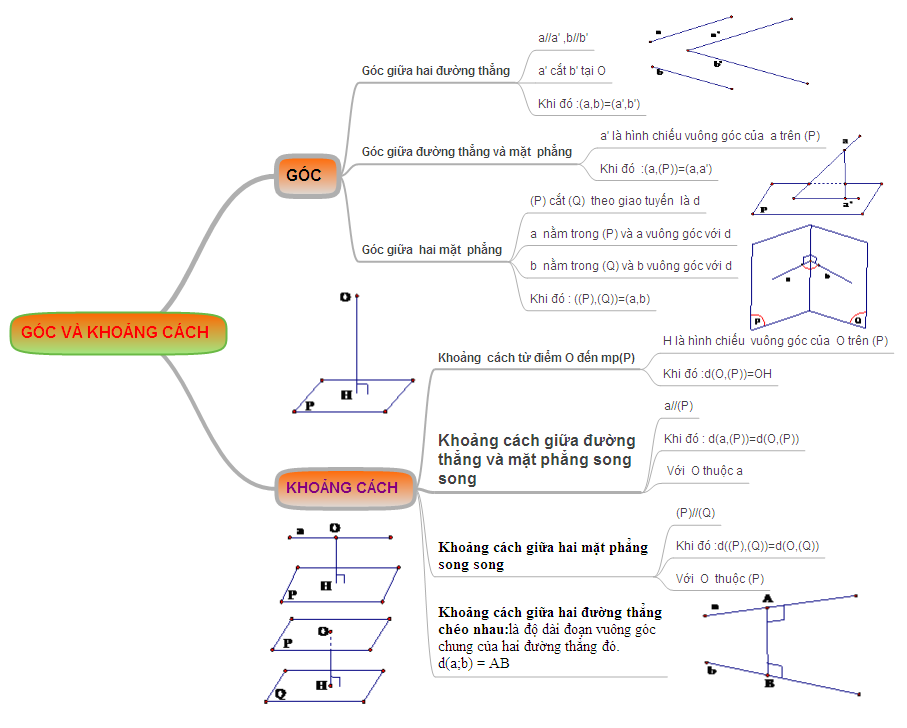
B. Bài tập minh họa
Bài 1: Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh (2asqrt{2}) và (AA'=asqrt{3}). Hình chiếu vuông góc của điểm A' trên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC. Tính theo a thể tích khối lăng trụ ABC.A'B'C' và khoảng cách từ điểm C đến mặt phẳng ABB'A'.
Hướng dẫn giải
- Tính ({V_{ABC.A'B'C'}}) .
Ta có (A'G bot left( {ABC} right) Rightarrow A'G) là chiều cao của lăng trụ ABC.A'B'C'.
Diện tích tam giác đều ABC là: ({S_{ABC}} = A{B^2}.frac{{sqrt 3 }}{4} = 2{a^2}sqrt 3).
Gọi M là trung điểm của BC, ta có: (AM = BC.frac{{sqrt 3 }}{2} = 2asqrt 2 .frac{{sqrt 3 }}{2} = asqrt 6).
(AG = frac{2}{3}AM = frac{{2asqrt 6 }}{3}).
Trong (Delta A'GA) vuông tại G, ta có (A'G = sqrt {A'{A^2} - A{G^2}} = sqrt {3{a^2} - frac{8}{3}{a^2}} = frac{{asqrt 3 }}{3}).
Vậy thể tích khối lăng trụ ABC.A'B'C' là:
({V_{ABC.A'B'C'}} = {S_{ABC}}.A'G = 2{a^3})
- Tính (dleft( {C,left( {ABB'A'} right)} right))
Gọi N là trung điểm của AB.
Trong (Delta A'GN), kẻ (GH bot A'N).
Chứng minh được (GH bot left( {ABB'A'} right)) tại H.
Suy ra (dleft( {G,left( {ABB'A'} right)} right) = GH).
Ta có (CN = AM = asqrt 6), (GN = frac{1}{3}CN = frac{{asqrt 6 }}{3}) .
(frac{1}{{G{H^2}}} = frac{1}{{A'{G^2}}} + frac{1}{{G{N^2}}} = frac{3}{{{a^2}}} + frac{9}{{6{a^2}}} = frac{9}{{2{a^2}}}) (Rightarrow GH = frac{{asqrt 2 }}{3}).
Do đó (dleft( {G,left( {ABB'A'} right)} right) = GH = frac{{asqrt 2 }}{3}).
Vậy (dleft( {C,left( {ABB'A'} right)} right) = 3dleft( {G,left( {ABB'A'} right)} right) = asqrt 2).
Bài 2: Cho hình chóp S.ABC, tam giác ABC vuông tại B, (AB = a , widehat{ ACB} = 60^0, SAperp (ABC)). Tính thể tích khối chóp S.ABC theo a và cosin của góc giữa hai mặt phẳng (SAC) và (SBC), biết khoảng cách từ điểm A đến mặt phẳng (SBC) bằng (frac{a}{2}).
Hướng dẫn giải
- Tính thể tích khối chóp S.ABC:
(begin{array}{l} left{ begin{array}{l} SA bot (ABC) Rightarrow BC bot SA BC bot AB end{array} right. Rightarrow BC bot (SAB) Rightarrow (SBC) bot (SAB). end{array})
Kẻ AH vuông góc SB ((H in SB)) suy ra: (AH bot (SBC) Rightarrow AH = frac{a}{2}.) (BC = frac{{AB}}{{tan {{60}^0}}} = frac{{asqrt 3 }}{3}.)
(frac{1}{{A{H^2}}} = frac{1}{{A{B^2}}} + frac{1}{{S{A^2}}} Rightarrow SA = frac{{asqrt 3 }}{3}.)
Diện tích tam giác ABC là: (S_{Delta ABC}=frac{a^2sqrt{3}}{6}).
Vậy thể tích khối chóp là: (V_{S.ABC}=frac{a^3}{18}.)
- Tính cosin của góc giữa hai mặt phẳng (SAC) và (SBC)
Kẻ (BI bot AC;,,IK bot SC.)
Ta có: (left{ begin{array}{l} BI bot AC BI bot SA end{array} right. Rightarrow BI bot (SAC) Rightarrow SC bot BI) (1)
Mặt khác: (IK bot SC) (2)
(SC bot (BIK) Rightarrow BK bot SC.) Suy ra góc giữa 2 mặt phẳng là (widehat{IKB}). Xét các tam giác vuông ABC và SBC ta tính được độ dài các đường cao:(BI=frac{a}{2};BK=frac{2asqrt{15}}{15}). Xét tam giác BIK vuông tại I ta có: (IK=frac{asqrt{15}}{30};coswidehat{IKB}=frac{1}{4}).
Bài 3: Cho hình chóp S.ABCD có thể tích bằng 48 và ABCD là hình thoi. Các điểm M, N, P, Q lần lượt là các điểm trên các đoạn SA, SB, SC, SD thỏa mãn: (SA = 2SM,SB = 3SN;) (SC = 4SP;SD = 5SQ.) Tính thể tích V của khối chóp S.MNPQ.
Hướng dẫn giải
.png)
Ta có: ({V_{SMNPQ}} = {V_{SMQP}} + {V_{SMNP}})
Và: ({V_{SADC}} = {V_{SQBC}} = frac{1}{2}{V_{S.ABCD}})
Mặt khác:
(begin{array}{l} frac{{{V_{S.MQP}}}}{{{V_{S.ADC}}}} = frac{{SQ}}{{SD}}.frac{{SM}}{{SA}}.frac{{SP}}{{SC}} = frac{1}{5}.frac{1}{2}.frac{1}{4} = frac{1}{{40}} Rightarrow {V_{S.MQP}} = frac{1}{{40}}.{V_{S.ADC}} = frac{1}{{80}}.{V_{S.ABCD}} end{array})
(begin{array}{l} frac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = frac{{SM}}{{SA}}.frac{{SP}}{{SC}}.frac{{SN}}{{SP}} = frac{1}{2}.frac{1}{4}.frac{1}{3} = frac{1}{{24}} Rightarrow {V_{S.MNP}} = frac{1}{{24}}{V_{S.ABC}} = frac{1}{{48}}.{V_{S.ABCD}} end{array})
(Rightarrow {V_{SMNPQ}} = left( {frac{1}{{80}} + frac{1}{{48}}} right){V_{S.ABCD}} = frac{8}{5})
Trắc nghiệm Hình học 12 Chương 1
- Trắc nghiệm Toán 12 Chương 1 Bài 1
- Trắc nghiệm Toán 12 Chương 1 Bài 2
- Trắc nghiệm Toán 12 Chương 1 Bài 3
- Trắc nghiệm ôn tập Chương 1 Toán 12
Đề kiểm tra Hình học 12 Chương 1
Đề kiểm tra trắc nghiệm online Chương 1 Hình học 12 (Thi Online)
Phần này các em được làm trắc nghiệm online trong vòng 45 phút để kiểm tra năng lực và sau đó đối chiếu kết quả và xem đáp án chi tiết từng câu hỏi.
- 40 câu hỏi trắc nghiệm về Khối đa diện Hình học lớp 12 năm học 2018 - 2019
- 40 câu trắc nghiệm ôn tập Chương 1 Hình học 12
- Đề kiểm tra 1 tiết Chương 1 Hình học 12 năm 2018 Trường THPT Đoàn Thượng
- Đề kiểm tra 1 tiết Chương 1 Hình học 12 năm 2018 Trường THPT Thị xã Quảng Trị
- Kiểm tra 1 tiết Trắc nghiệm Khối đa diện Hình học 12 năm học 2017 - 2018
Đề kiểm tra Chương 1 Hình học 12 (Tải File)
Phần này các em có thể xem online hoặc tải file đề thi về tham khảo gồm đầy đủ câu hỏi và đáp án làm bài.
- Đề kiểm tra 1 tiết Chương 1 Hình 12 năm 2017-Trường THPT Hùng Vương
- Đề kiểm tra 1 tiết chương 1 lần 2 Hình học lớp 12 Trường THPT Trần Hưng Đạo năm 2017
- Đề kiểm tra 1 tiết Chương 1 Hình học 12 năm 2017 - Trường THPT Tôn Thất Tùng có đáp án
- Đề kiểm tra 1 tiết Chương 1 Hình học 12 năm 2017 -Trường THPT Cát Tiên
- Đề kiểm tra 1 tiết Chương 1 Hình học Lớp 12 năm 2017 Trường THPT Nguyễn Trung Trực
Lý thuyết từng bài Chương 1 và hướng dẫn giải bài tập SGK
Lý thuyết các bài học Hình học 12 Chương 1
- Hình học 12 Bài 1 Khái niệm về khối đa diện
- Hình học 12 Bài 2 Khối đa diện lồi và khối đa diện đều
- Hình học 12 Bài 3 Khái niệm về thể tích của khối đa diện
- Hình học 12 Ôn tập chương 1 Khối đa diện
Hướng dẫn giải bài tập Toán 12 Chương 1
- Giải bài tập Toán 12 Chương 1 Bài 1
- Giải bài tập Toán 12 Chương 1 Bài 2
- Giải bài tập Toán 12 Chương 1 Bài 3
- Giải bài ôn tập Chương 1 Toán 12
Trên đây là tài liệu Ôn tập Hình học 12 Chương 1. Hy vọng với tài liệu này, các em sẽ giúp các em ôn tập và hệ thống lại kiến thức Chương 1 thật tốt. Để thi online và tải file đề thi về máy các em vui lòng đăng nhập vào trang hoc247.net và ấn chọn chức năng "Thi Online" hoặc "Tải về". Ngoài ra, các em còn có thể chia sẻ lên Facebook để giới thiệu bạn bè cùng vào học, tích lũy thêm điểm HP và có cơ hội nhận thêm nhiều phần quà có giá trị từ HỌC247 !
Link nội dung: https://khangdienreal.vn/on-tap-chuong-1-hinh-12-a66694.html